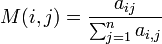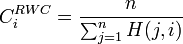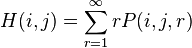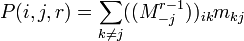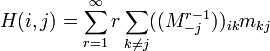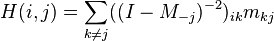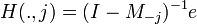Random-Walk Closeness Centrality
Definition
Consider a weighted network – either directed or undirected – with n nodes
denoted by j=1, …, n; and a random walk process on this network with a
transition matrix M. The
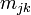 element of M describes the probability of the random walker that has reached
node i, proceeds directly to node j. These probabilities are defined in the
following way.
element of M describes the probability of the random walker that has reached
node i, proceeds directly to node j. These probabilities are defined in the
following way.
where
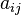 is the (i,j)th element of the weighting matrix A of the network. When there is
no edge between two nodes, the corresponding element of the A matrix is zero.
is the (i,j)th element of the weighting matrix A of the network. When there is
no edge between two nodes, the corresponding element of the A matrix is zero.
The random walk closeness centrality of a node i is the inverse of the average mean first passage time to that node:
Mean first passage time
The mean first passage time from node i to node j is the expected number of steps it takes for the process to reach node j from node i for the first time:
where P(i,j,r) denotes the probability that it takes exactly r steps to reach
j from i for the first time. To calculate these probabilities of reaching a node
for the first time in r steps, it is useful to regard the target node as an
absorbing one, and introduce a transformation of M by deleting its j-th row and
column and denoting it by
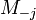 .
As the probability of a process starting at i and being in k after r-1 steps is
simply given by the (i,k)th element of
.
As the probability of a process starting at i and being in k after r-1 steps is
simply given by the (i,k)th element of
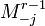 ,
P(i,j,r) can be expressed as
,
P(i,j,r) can be expressed as
Substituting this into the expression for mean first passage time yields
Using the formula for the summation of geometric series for matrices yields
where I is the n-1 dimensional identity matrix.
For computational convenience, this expression can be vectorized as
where
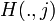 is the vector for first passage times for a walk ending at node j, and e is an
n-1 dimensional vector of ones.
is the vector for first passage times for a walk ending at node j, and e is an
n-1 dimensional vector of ones.
Mean first passage time is not symmetric, even for undirected graphs.
[Random walk closeness centrality. (2013, March 7). In Wikipedia]
Software
References
- NOH, J. D. & RIEGER, H. 2004. Random walks on complex networks. Physical review letters, 92, 118701.
- Random walk closeness centrality. (2013, March 7). In Wikipedia, The Free Encyclopedia. Retrieved 07:56, August 6, 2014, from http://en.wikipedia.org/w/index.php?title=Random_walk_closeness_centrality&oldid=542550793