There are no comment yet.
PeC Centrality
Definition
PeC, is proposed based on the integration of protein-protein interaction data and gene expression data. The
basic ideas behind PeC are as follows:
The probability that two proteins are co-clustered and co-expressed is evaluated based on the edge clustering coefficient (ECC) and pearson correlation coefficient (PCC).
New centrality measure PeC by integration of PCC and ECC. It has been proved that there exist a number of protein complexes which play a key role in carrying out biological functionality and the essentiality tends to be a product of a protein complex rather than an individual protein.
Based on the definitions of edge clustering coefficient (ECC) and pearson’s correlation coefficient (PCC), they propose a new centrality measure which is named as PeC. The probability that two proteins are coclustered is described from a topological view and the probability that two proteins are co-clustered is characterized from a biological view. Thus, we defined the probability of paired proteins u and v to be in the same cluster as following:
For a protein v, its PeC(v) is defined as the sum of the probabilities that the protein and its neighbors belong to a same cluster: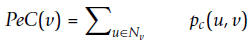 Where Nv denotes the set of all
neighbors of node v. The value of PeC(v) is determined by not only how many
neighbors the protein has but also how likely it is co-clustered with its
neighbors.
Where Nv denotes the set of all
neighbors of node v. The value of PeC(v) is determined by not only how many
neighbors the protein has but also how likely it is co-clustered with its
neighbors.
- A highly connected protein is more likely to be essential than a low connected one;
- Essential proteins tend to form densely connected clusters;
- Essential proteins in the same cluster have a more chance to be co-expressed.
The probability that two proteins are co-clustered and co-expressed is evaluated based on the edge clustering coefficient (ECC) and pearson correlation coefficient (PCC).
New centrality measure PeC by integration of PCC and ECC. It has been proved that there exist a number of protein complexes which play a key role in carrying out biological functionality and the essentiality tends to be a product of a protein complex rather than an individual protein.
Based on the definitions of edge clustering coefficient (ECC) and pearson’s correlation coefficient (PCC), they propose a new centrality measure which is named as PeC. The probability that two proteins are coclustered is described from a topological view and the probability that two proteins are co-clustered is characterized from a biological view. Thus, we defined the probability of paired proteins u and v to be in the same cluster as following:
pc(u, v)= ECC(u, v) × PCC(u, v)
For a protein v, its PeC(v) is defined as the sum of the probabilities that the protein and its neighbors belong to a same cluster:
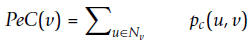
Software
- From authors:
Download PeC.zip
References
- LI, M., ZHANG, H., WANG, J.-X. & PAN, Y. 2012. A new essential protein discovery method based on the integration of protein-protein interaction and gene expression data. BMC systems biology, 6, 15.