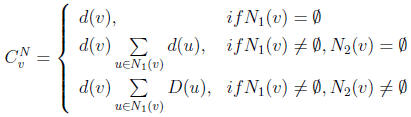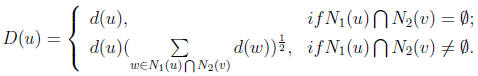Neighbor Based Centrality
Definition
We can imagine that there are information flows between two connected nodes in a network,
Each node u receives some amount of information from each its adjacent node v , and each its
adjacent node V also receives some amount of information from each of its node w. Thus the
total amount of information received of node u is dependent to not only its all adjacent nodes
called its first layer neighbors, but also all those nodes which are the adjacent neighbors of its first
layer neighbors and not the first layer neighbors. This kind of the adjacent neighbors of the first
layer neighbors of node u are called the second layer neighbors of node u. Therefore, the amount
of information received by node u is proportional to not only the degree of its first layer adjacent
node. Then, the more the total amount of information received by a node (or a group of nodes),
the more important the node (the group of the nodes) will be. Note that the total amount of
information received of a node is dependent on not only its adjacent nodes, but also those nodes
which have the same adjacent nodes as this node. Thus, if a node receives more information from
its adjacent nodes and the nodes which have the same adjacent nodes as this node, then the node
is more important (central).
Neighbor based centrality of node v, denoted by CNv, is defined by: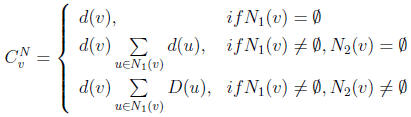 where
where
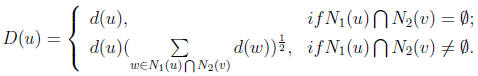 where d(j) denotes the degree of node j and
N1(v) is a set of the first layer neighbors of node v and
N2(v) is a set of the second layer neighbors of nodes in N1(v) set.
where d(j) denotes the degree of node j and
N1(v) is a set of the first layer neighbors of node v and
N2(v) is a set of the second layer neighbors of nodes in N1(v) set.
Neighbor based centrality of node v, denoted by CNv, is defined by: