κ-Path Centrality
Definition
κ-path node centrality
For each node v of a graph G = (V,E), the κ-path node centrality Cκ(v) of v is defined as the sum, over all possible source nodes s, of the frequency with which a message originated from s goes through v, assuming that the message traversals are only along random simple paths of at most κ edges.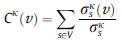 where s are all the possible source nodes, σκs(v) is the number of κ-paths
originating from s and passing through v and σκs is the overall number of κ-paths originating from s.
where s are all the possible source nodes, σκs(v) is the number of κ-paths
originating from s and passing through v and σκs is the overall number of κ-paths originating from s.
See Geodesic K-Path Edge Centrality
See Geodesic K-Path Centrality
k-Path centrality with random-algorithm approach
Taniarza, N. and Maharani, W., 2018, March. Social network analysis using k-Path centrality method. In Journal of Physics: Conference Series (Vol. 971, No. 1, p. 012015). IOP Publishing.
For each node v of a graph G = (V,E), the κ-path node centrality Cκ(v) of v is defined as the sum, over all possible source nodes s, of the frequency with which a message originated from s goes through v, assuming that the message traversals are only along random simple paths of at most κ edges.
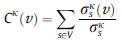
See Geodesic K-Path Edge Centrality
See Geodesic K-Path Centrality
k-Path centrality with random-algorithm approach
Taniarza, N. and Maharani, W., 2018, March. Social network analysis using k-Path centrality method. In Journal of Physics: Conference Series (Vol. 971, No. 1, p. 012015). IOP Publishing.
Software
References
- Alahakoon, T., Tripathi, R., Kourtellis, N., Simha, R. and Iamnitchi, A., 2011, April. K-path centrality: A new centrality measure in social networks. In Proceedings of the 4th workshop on social network systems (p. 1). ACM.
DOI: 10.1145/1989656.1989657
