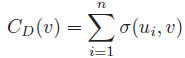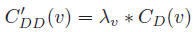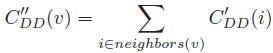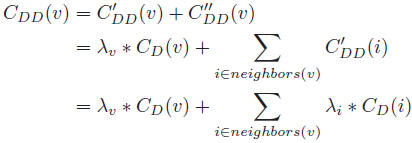Diffusion Degree
Definition
The degree centrality of node v can be defined as:
- σ(ui, v) = 1 if and only if ui and v are connected and = 0 otherwise.
References
- KUNDU, S., MURTHY, C. A. & PAL, S. K. 2011. A New Centrality Measure for Influence Maximization in Social Networks. In: KUZNETSOV, S., MANDAL, D., KUNDU, M. & PAL, S. (eds.) Pattern Recognition and Machine Intelligence. Springer Berlin Heidelberg.
- PAL, S. K., KUNDU, S. & MURTHY, C. 2014. Centrality Measures, Upper Bound, and Influence Maximization in Large Scale Directed Social Networks. Fundamenta Informaticae, 130, 317-342.