Bargaining Centrality
Definition
In bargaining situations, it is advantageous to be connected to those who have few options; power comes from being connected to those who are powerless. Being connected to powerful people who have many competitive trading partners weakens one’s own bargaining power.
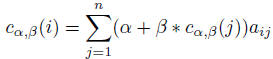and in matrix notation:
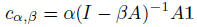where α is a scaling factor, β is the influence parameter, A is the adjacency matrix, and is the n-dimentional vector in which every entry is 1.
Bonacich suggests a value such that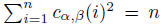
holds. Therefore only the second parameter β is of interest. This parameter may be chosen either positive or negative, covering positive or negative influence, respectively. The choice β = 0 leads to a trivial solution where the centrality correlates with the degree of the vertices. A negative value for β may lead to negative values for the centralities of the vertices. Additionally it follows from the equation that the larger |β| the higher the impact of the structure of the network on the centrality index is.
Above equation is solvable if the inverse of (I − βA) exists and this inverse exists if no eigenvalue of A is equal to 1.
The magnitude of β should reflect the degree to which authority or communication is transmitted locally or globally throughout the network as a whole. Small values of β give more weight to the local structure, whereas large values are more cognizant of the position of individuals at the global level. Therefore, a person can be powerful if he or she is in contact with trading partners who have no options or if his or her other optional trading partners themselves also have many other options.
The magnitude of β reflects the radius of power. Small values of β weight local structure, Larger values weight global structure.
If β > 0, ego has higher centrality when tied to people who are central.
If β < 0, then ego has higher centrality when tied to people who are not central.
With β = 0, you get degree centrality.
Interpretively, the Bonacich power measure corresponds to the notion that the power of a vertex is recursively defined by the sum of the power of its alters. The nature of the recursion involved is then controlled by the power exponent: positive values imply that vertices become more powerful as their alters become more powerful (as occurs in cooperative relations), while negative values imply that vertices become more powerful only as their alters become weaker (as occurs in competitive or antagonistic relations). The magnitude of the exponent indicates the tendency of the effect to decay across long walks; higher magnitudes imply slower decay. One interesting feature of this measure is its relative instability to changes in exponent magnitude (particularly in the negative case). If your theory motivates use of this measure, you should be very careful to choose a decay parameter on a non-ad hoc basis.
Bonacich’s Bargaining Centrality is not restricted to positive feedback concept and supports both, the positive influence as seen for example in communication networks, and the negative influence as seen in bargaining situations. In bargaining situations a participant is strong if he is connected to individuals having no other options and are therefore weak. Bonacich’s bargaining centrality is defined for unweighted and directed graphs G = (V,E) without loops. Therefore the adjacency matrix is not necessarily symmetric and contains only zeros and ones.
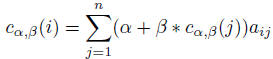
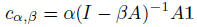
Bonacich suggests a value such that
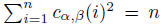holds. Therefore only the second parameter β is of interest. This parameter may be chosen either positive or negative, covering positive or negative influence, respectively. The choice β = 0 leads to a trivial solution where the centrality correlates with the degree of the vertices. A negative value for β may lead to negative values for the centralities of the vertices. Additionally it follows from the equation that the larger |β| the higher the impact of the structure of the network on the centrality index is.
Above equation is solvable if the inverse of (I − βA) exists and this inverse exists if no eigenvalue of A is equal to 1.
The magnitude of β should reflect the degree to which authority or communication is transmitted locally or globally throughout the network as a whole. Small values of β give more weight to the local structure, whereas large values are more cognizant of the position of individuals at the global level. Therefore, a person can be powerful if he or she is in contact with trading partners who have no options or if his or her other optional trading partners themselves also have many other options.
The magnitude of β reflects the radius of power. Small values of β weight local structure, Larger values weight global structure.
If β > 0, ego has higher centrality when tied to people who are central.
If β < 0, then ego has higher centrality when tied to people who are not central.
With β = 0, you get degree centrality.
Interpretively, the Bonacich power measure corresponds to the notion that the power of a vertex is recursively defined by the sum of the power of its alters. The nature of the recursion involved is then controlled by the power exponent: positive values imply that vertices become more powerful as their alters become more powerful (as occurs in cooperative relations), while negative values imply that vertices become more powerful only as their alters become weaker (as occurs in competitive or antagonistic relations). The magnitude of the exponent indicates the tendency of the effect to decay across long walks; higher magnitudes imply slower decay. One interesting feature of this measure is its relative instability to changes in exponent magnitude (particularly in the negative case). If your theory motivates use of this measure, you should be very careful to choose a decay parameter on a non-ad hoc basis.
Bonacich’s Bargaining Centrality is not restricted to positive feedback concept and supports both, the positive influence as seen for example in communication networks, and the negative influence as seen in bargaining situations. In bargaining situations a participant is strong if he is connected to individuals having no other options and are therefore weak. Bonacich’s bargaining centrality is defined for unweighted and directed graphs G = (V,E) without loops. Therefore the adjacency matrix is not necessarily symmetric and contains only zeros and ones.
Requirements
Require directed and loop free network.
Software
References
- BONACICH, P. 1987. Power and centrality: A family of measures. American journal of sociology, 1170-1182.
- BRANDES, U. & ERLEBACH, T. 2005. Network Analysis: Methodological Foundations, U.S. Government Printing Office.
- ZHANG, A. 2009. Protein Interaction Networks: Computational Analysis, Cambridge University Press.